Exploring Expectancy in Trading: Breaking It Down
The path to profits
One of the most important things when it comes to trend following and backtesting is expectancy.
“The goal of a successful trader is to make the best trades. Money is secondary.”
– Alexander Elder
Understanding Expectancy
Expectancy serves as a cornerstone in the realm of trading, offering traders a lens to gauge the potential profitability of their strategies over time. By understanding expectancy, traders can effectively evaluate their strategies and make well-informed decisions regarding their approach.
What is Expectancy?
In the context of trading, expectancy stands as a statistical metric, estimating the average gains or losses a trader can anticipate per trade, rooted in their historical performance. It amalgamates the win rate (the proportion of profitable trades) and the risk-reward ratio (the ratio of average gains to average losses).
Significance of expectancy
The importance of expectancy in trading shows across various facets:
Strategy Evaluation: Expectancy facilitates a methodical assessment of trading strategies. A positive expectancy indicates profitability over the long haul, while a negative one signals potential losses.
Informed Decision-Making: Armed with an understanding of expectancy, traders can judiciously decide whether to persist with a specific strategy, tweak it, or explore alternative avenues.
Emotional Management: Expectancy lends traders a statistical foundation for their decisions, fostering a disciplined approach and mitigating emotional biases. Letting go of the thought that every trade needs to be a winner.
Risk Mitigation: By computing expectancy, traders can calibrate position sizes prudently, aligning them with their performance and risk tolerance levels.
Crunching the Numbers: Calculating Expectancy
The calculation of expectancy necessitates three key inputs:
Win Rate: The proportion of winning trades.
Average Win: The mean gain from profitable trades.
Average Loss: The average loss incurred from unprofitable trades.
Expectancy is computed using the formula:
Expectancy = (Win Rate × Average Win) - ((1 - Win Rate) × Average Loss)
For instance, if a trader boasts a 60% win rate, with an average win of $100 and an average loss of $50, their expectancy would be:
Expectancy = (0.6 × $100) - ((1 - 0.6) × $50)
Expectancy = $60 - $20
Expectancy = $40
This implies that, on average, the trader can anticipate a $40 profit per trade over time.
Embracing Positive Expectancy
Positive expectancy is very important in trading, harmonizing seemingly conflicting directives such as "cut loses" and "let winners run." Ultimately, it underscores the essence of sustainable trading strategies.
Enhancing Your Expectancy
Traders can fortify their expectancy through various strategies:
Optimization of Risk-Reward Ratio: Emphasis on enhancing the average gains of profitable trades or curbing losses can be pivotal. Effective risk management techniques, like entry and exit strategies play a pivotal role.
Diversification: Broadening the spectrum of trading strategies and instruments can mitigate risk by dispersing it across diverse markets, thereby elevating overall expectancy. This is why we trade so many positions.
In essence, expectancy stands as a beacon guiding traders through the labyrinth of trading, offering clarity amidst the complexities, and paving the path toward sustained profitability.
The most important lesson
A high win rate does not equal bigger profits.
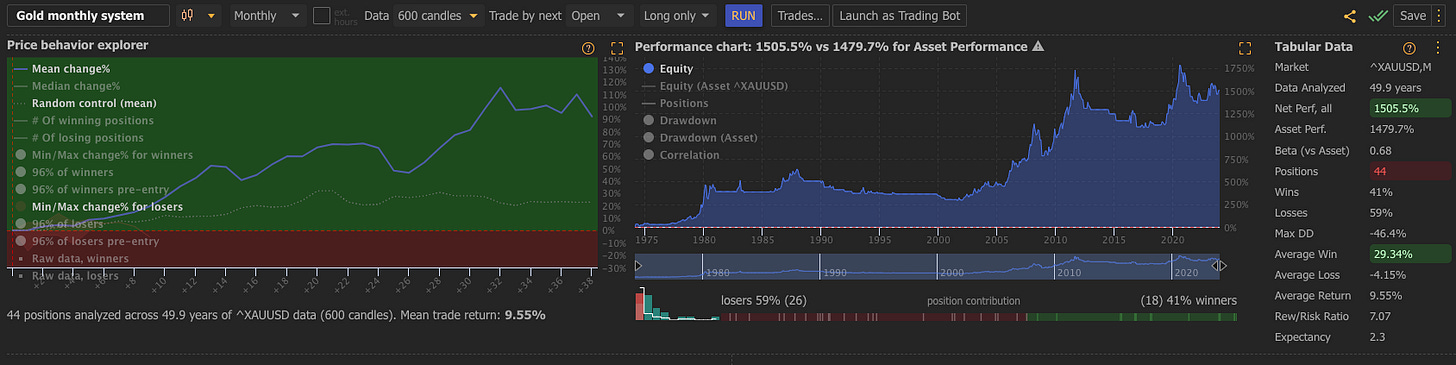
A very simple long term strategy that outperforms gold over time with shallow drawdowns. (If you run the system long and short your returns are doubled) This strategy has a 40% win rate.
Every trade does not need to be a winner you just need your risk to reward skewed in to your favor.
Stay informed. Stay resilient. Against all odds.
Warm regards, Jason Perz
If you find this content valuable, please consider liking, sharing, and subscribing.
Feel free to pass it along if you think it can benefit others.
YouTube: @againstalloddsresearch https://www.youtube.com/channel/UCLvDNCnhNQbQnABUSFbwagg
Twitter: @jasonp138
Substack: aaoresearch.substack.com
Against All Odds Research
jperz1985@icloud.com



ah yes, I'm reading Van Tharp now. It's interesting that he places quite a lot of emphasis on the variability of losses dividing expectancy by std dev(R) to get a System Quality Number.